Q-Q plot in Python

Renesh Bedre    1 minute read

The Q-Q plot (Quantile-Quantile plot) is commonly used to assess whether sample data follows a specific theoretical distribution (in most cases normal distribution).

Q-Q plot compares the observed quantiles of the sample data and expected quantiles of the theoretical distribution.

The following figures compare the Q-Q plots for data that follows normal distribution versus the data that does not follow normal distribution.

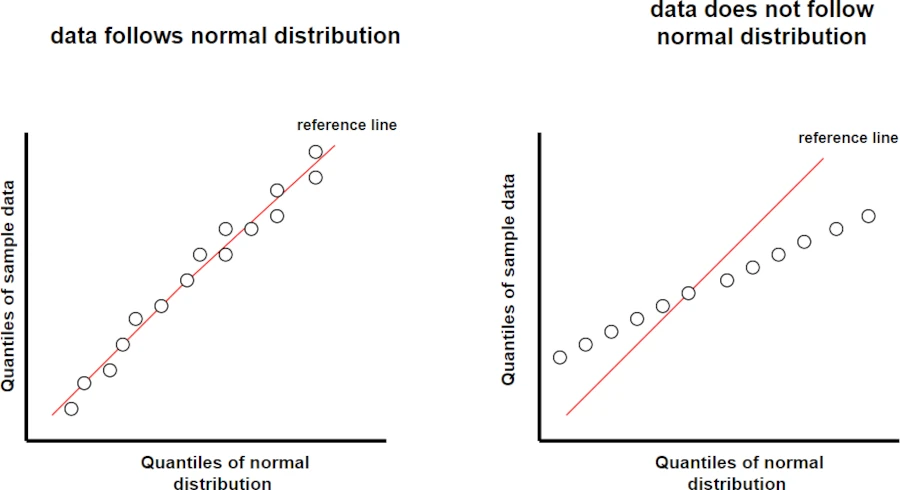
QQ plot

If the sample data is from normal distribution, you should see sample quantiles follow the expected quantiles in a straight line (also known as reference line).

Here’s a detailed example of how to create a Q-Q plot in Python using statsmodels

Generate random dataset with approximate normal distribution,

# import package
import numpy as np

# genrate dataset with normal distribution
norm_data = np.random.normal(loc=0, scale=1, size=500)

Now, generate a Q-Q plot using qqplot() function from statsmodels in Python,

Note: By default, the qqplot() function compares the sample data quantiles with standard normal distribution quantiles.

# import package
import statsmodels.api as sm
import matplotlib.pyplot as plt

# create Q-Q plot with 45-degree line (reference line)
sm.qqplot(norm_data, line='45')
plt.xlabel("Theoretical Quantiles")
plt.ylabel("Sample Quantiles")
plt.show()

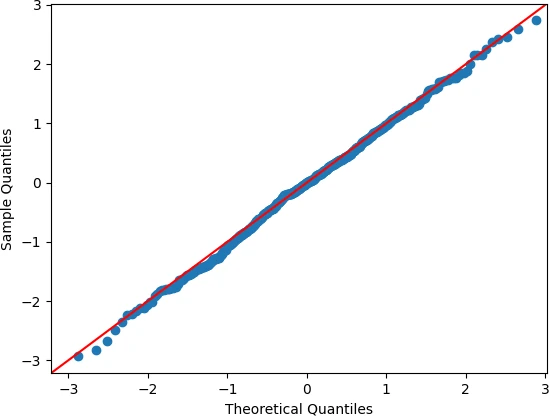
Q-Q plot in Python

From the Q-Q plot, you can see that the observed quantiles of sample data follow the reference line, and we conclude that the sample dataset follows a normal distribution.

In addition to the Q-Q plot, you should also assess whether the dataset follows a normal distribution using a statistical test such as the Shapiro-Wilk test.



Enhance your skills with courses on Statistics and Python


This work is licensed under a Creative Commons Attribution 4.0 International License

Some of the links on this page may be affiliate links, which means we may get an affiliate commission on a valid purchase. The retailer will pay the commission at no additional cost to you.

You may also enjoy